Preliminaries
Structured prediction
| I | studied | in | London | with | Sebastian | Riedel |
|---|---|---|---|---|---|---|
| PRP | VBD | IN | NNP | IN | NNP | NNP |
| O | O | O | B-LOC | O | B-PER | I-PER |
- part of speech (PoS) tagging
- named entity recognition (NER)
Input: a sentence $\mathbf{x}=[x_1...x_N]$
Output: a sequence of labels $\mathbf{y}=[y_{1}\ldots y_{N}] \in {\cal Y}^N$
Structured prediction
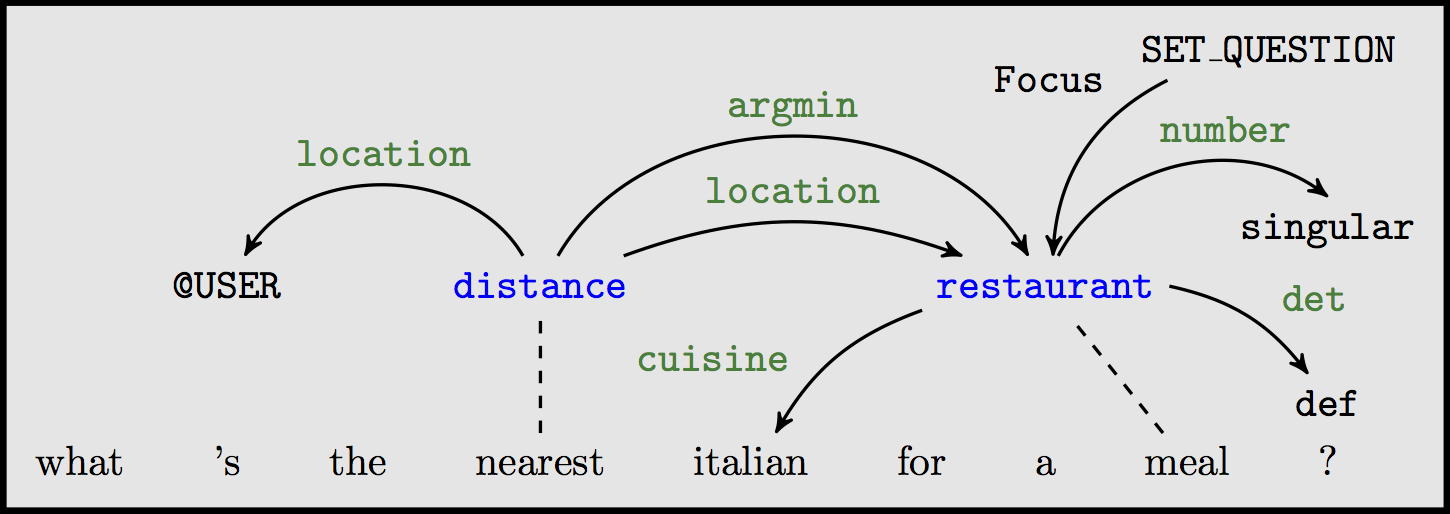
Semantic parsing, but also syntactic parsing, semantic role labeling, question answering over knowledge bases, etc.)
Input: a sentence $\mathbf{x}=[x_1...x_N]$
Output: a meaning representation graph $\mathbf{G}=(V,E) \in {\cal G_{\mathbf{x}}}$
Structured prediction

Natural language generation (NLG), but also summarization, decoding in machine translation, etc.
Input: a meaning representation
Output: $\mathbf{w}=[w_1...w_N], w\in {\cal V}\cup END, w_N=END$
Incremental modeling, a.k.a:
- local
- greedy
- pipeline
- transition-based
- history-based
Joint modeling¶
A model (e.g. conditional random field) that scores complete outputs (e.g. label sequences):
$$\mathbf{\hat y} =\hat y_{1}\ldots \hat y_{N} = \mathop{\arg \max}_{Y \in {\cal Y}^N} f(y_{1}\ldots y_{N}, \mathbf{x})$$- exhaustive exploration of the search space
- large/complex search spaces are challenging
- efficient dynamic programming restricts modelling flexibility (i.e. Markov assumptions)
Incremental modeling¶
A classifier predicting a label at a time given the previous ones:
\begin{align} \hat y_1 &=\mathop{\arg \max}_{y \in {\cal Y}} f(y, \mathbf{x}),\\ \mathbf{\hat y} = \quad \hat y_2 &=\mathop{\arg \max}_{y \in {\cal Y}} f(y, \mathbf{x}, \hat y_1), \cdots\\ \hat y_N &=\mathop{\arg \max}_{y \in {\cal Y}} f(y, \mathbf{x}, \hat y_{1} \ldots \hat y_{N-1}) \end{align}- use our favourite classifier
- no restrictions on features
- prone to error propagation (i.i.d. assumption broken)
- local model not trained wrt the task-level loss
Imitation learning¶
Improve incremental modeling to:
- address error-propagation
- train wrt the task-level loss function
Meta-learning: use our favourite classifier and features, but generate better (non-i.i.d.) training data
To apply IL we need:
- transition system (what our classifier can do)
- task loss (what we optimize for)
- expert policy (the teacher to help us)
Transition system
The actions $\cal A$ the classifier $f$ can predict and their effect on the state which tracks the prediction: $S_{t+1}=S_1(\alpha_1\ldots\alpha_t)$
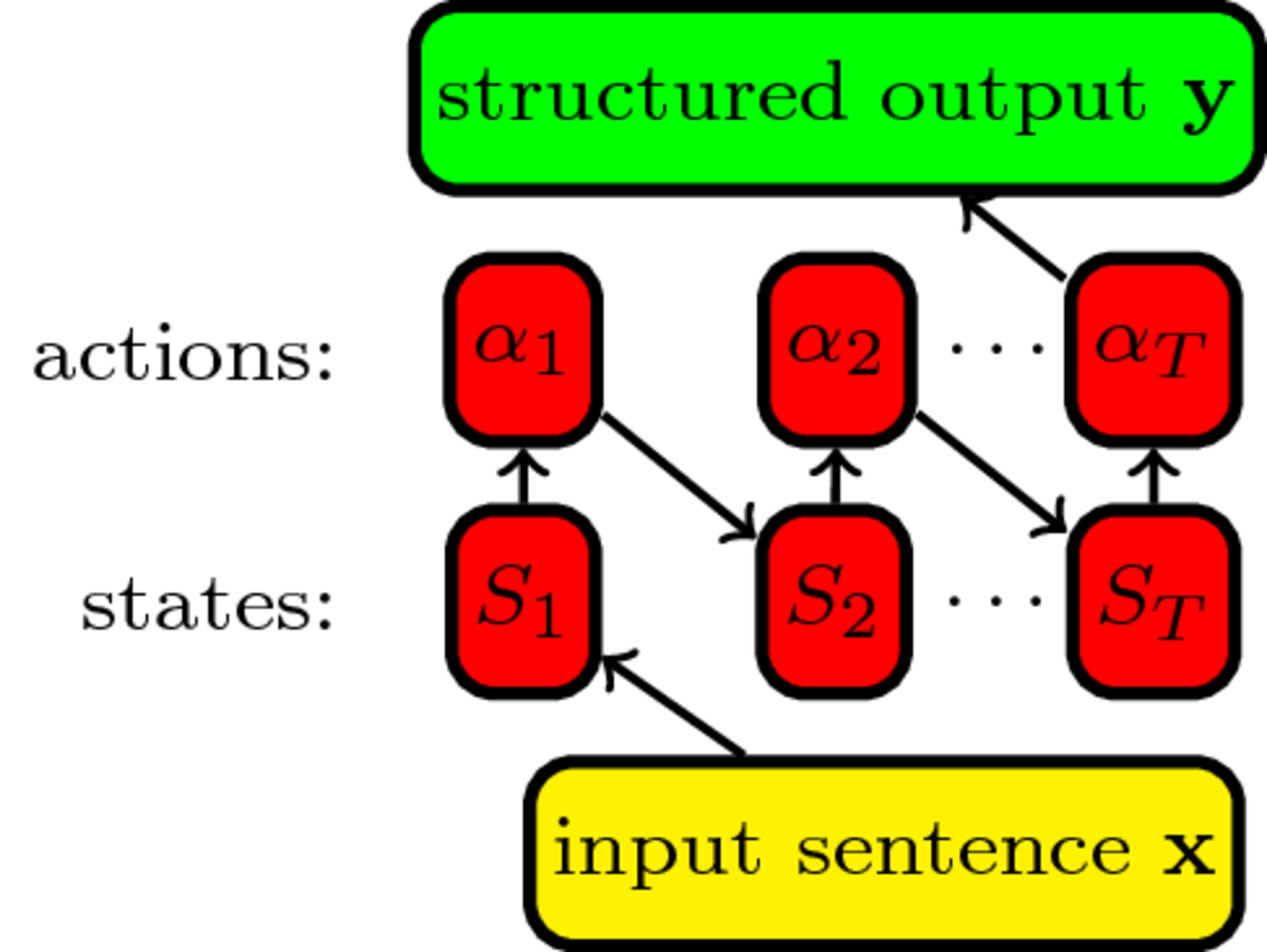
Transition system
\begin{align} & \textbf{Input:} \; sentence \; \mathbf{x}\\ & state \; S_1=initialize(\mathbf{x}); timestep \; t = 1\\ & \mathbf{while}\; S_t \; \text{not final}\; \mathbf{do}\\ & \quad action \; \alpha_t = \mathop{\arg \max}_{\alpha \in {\cal A}} f(\alpha, \mathbf{x})\\ & \quad S_{t+1}=S_t(\alpha_t); t=t+1\\ \end{align}
- PoS/NER tagging? for each word, left-to-right, predict a PoS tag which is added to the output
- NLG? predict a word adding it to the output until the
EndOfSentenceis predicted
Supervising the classifier¶
What are good actions in incremental structured prediction?
Those that reach $S_{final} = S_1(\alpha_1\ldots\alpha_T)$ with low task loss:
$$loss = L(S_{final}, \mathbf{y}) \geq 0$$- PoS tagging? Hamming loss: number of incorrect tags
- NER? number of false positives and false negatives
- NLG? BLEU: % of n-grams predicted present in the gold reference(s), i.e. $L=1-BLEU(S_{final}, \mathbf{y})$
Action assessment¶
| I | studied | in | London | with | Sebastian | Riedel |
|---|---|---|---|---|---|---|
| PRP | VBD | IN | NNP | IN | NNP | NNP |
| O | O | O | B-LOC | O | B-PER | I-PER |
How many incorrect PoS tags due to $\alpha_6$ being NNP? 0
How many $FP+FN$ due to $\alpha_6$ being B-PER?
Depends! If $\alpha_7$ is
- I-PER: $0$ (correct)
- O: $2$ (1FP+1FN)
- B-*: $3$ (2FP+1FN)
More action assessment¶
Can we tell how predicting a word will change our BLEU? $$ BLEU([\alpha_1...\alpha_T],\mathbf{y}) = \prod_{n=1}^N \frac{\# \text{n-grams} \in ([\alpha_1...\alpha_T] \cap \mathbf{y})}{\# \text{n-grams} \in [\alpha_1..\alpha_T]} $$
No! (assuming N>1)
Non-decomposable losses wrt transition system are common!
Imitation learning trains incremental models for such losses
Affects joint models too: loss does not always decompose over the graphical model (Tarlow and Zemel, 2012)
Expert policy¶
Returns the best action at the current state by looking at the gold standard assuming future actions are also optimal:
$$\alpha^{\star}=\pi^{\star}(S_t, \mathbf{y}) = \mathop{\arg \min}_{\alpha \in {\cal A}} L(S_t(\alpha,\pi^{\star}),\mathbf{y})$$| I | studied | in | London | with | Sebastian | Riedel |
|---|---|---|---|---|---|---|
| PRP | VBD | IN | NNP | IN | NNP | NNP |
PoS tagging: $\pi^{\star}(S_t, \mathbf{y})= \pi^{\star}(S_t, [y_1...y_T])=y_t$
Expert policy¶
What action should $\pi^{\star}$ return?
| I | studied | in | London | with | Sebastian | Riedel |
|---|---|---|---|---|---|---|
| O | O | O | B-LOC | O | B-PER | I-PER |
| O | O | O | B-LOC | O | O | O |
Takes previous actions into account to be optimal (dynamic)
Finding the optimal action can be expensive.
IL can learn with sub-optimal experts!
Cost-sensitive classification¶
Each action has a different cost:
| O | B-PER | I-PER | B-LOC | I-LOC | B-ORG | I-LOC |
|---|---|---|---|---|---|---|
| 1 | 2 | 2 | 0 | 1 | 1 | 1 |
Learning with costs:
- sample instances according to their cost to train any classifier (Abe et al., 2004)
- in error-driven learning adjust the updates in proportion to the error cost (Crammer et al., 2006)
