Imitation learning

Imitation learning for part-of-speech tagging

I	can	fly
Pronoun	Modal	Verb

Task loss: Hamming loss: number of incorrectly predicted tags

Transition system: Tag each token left-to-right

Expert policy: Return the next tag from the gold standard

Gold standard in search space

paths = [[],[(0,4),(1,3)],[(0,4),(1,3),(2,2)],[(0,4),(1,3),(2,2),(3,1)]]
rows = ['Noun', 'Verb', 'Modal', 'Pronoun','NULL']
columns = ['NULL','I', 'can', 'fly']
cbs = []
for path in paths:
    cbs.append(cg.draw_cost_breakdown(rows, columns, path))
util.Carousel(cbs)

Previous   Next

• Three actions to complete the output
• Expert policy replicates the gold standard

Training a classifier with structure features

gold_path = [(0,4),(1,3),(2,2),(3,1)]
cb_gold = cg.draw_cost_breakdown(rows, columns, gold_path)
cb_gold

timestep	label ($\alpha_t$)	features ($\phi(S_{t-1},\mathbf{x})$)
$t=1$	Pronoun	token=I, ..., prev=NULL
$t=2$	Modal	token=can, ..., prev=Pronoun
$t=3$	Verb	token=fly, ..., prev=Modal

Algorithm

\begin{align} & \textbf{Input:} \; D_{train} = \{(\mathbf{x}^1,\mathbf{y}^1)...(\mathbf{x}^M,\mathbf{y}^M)\}, \; \text{expert}\; \pi^{\star}, \; \text{classifier} \; H\\ & \text{set training examples}\; \cal E = \emptyset\\ & \mathbf{for} \; (\mathbf{x},\mathbf{y}) \in D_{train} \; \mathbf{do}\\ & \quad \text{generate expert trajectory} \; \alpha_1^{\star}\dots \alpha_T^{\star} = \pi^{\star}(\mathbf{x},\mathbf{y})\\ & \quad \mathbf{for} \; \alpha^{\star}_t \in \alpha_1^{\star}\dots \alpha_T^{\star} \; \mathbf{do}\\ & \quad \quad \text{extract features}\; \mathit{feat}=\phi(\mathbf{x},S_{t-1}) \\ & \quad \quad \cal E = \cal E \cup (\mathit{feat},\alpha^{\star}_t)\\ & \text{learn} \; H\; \text{from}\; \cal E\\ \end{align}

With logistic regression and $k$ previous tags: training a $kth$-order Maximum Entropy Markov Model (McCallum et al., 2000)

Exposure bias

wrong_path = [(0,4),(1,3),(2,1)]
cb_wrong = cg.draw_cost_breakdown(rows, columns, wrong_path)
util.Carousel([cb_gold, cb_wrong])

Previous   Next

We had seen:   

timestep	label	features
t=3	Verb	token=fly,..., prev=Modal

but not:   

timestep	label	features
t=3	Verb	token=fly,..., prev=Verb

Addressing exposure with Rollins

Allow the classifier to guide the learning

Define a rollin policy that sometimes uses the expert $\pi^{\star}$ and other times the classifier $H$:

$$\pi^{in} = \beta\pi^{\star} + (1-\beta)H$$

DAgger algorithm

\begin{align} & \textbf{Input:} \; D_{train} = \{(\mathbf{x}^1,\mathbf{y}^1)...(\mathbf{x}^M,\mathbf{y}^M)\}, \; \text{expert}\; \pi^{\star}, \; \text{classifier} \; H\\ & \text{set training examples}\; \cal E = \emptyset ,\; \color{red}{\pi^{\star}\; \mathrm{probability}\; \beta=1}\\ & \mathbf{while}\; \text{termination condition not reached}\; \mathbf{do}\\ & \quad \color{red}{\text{set rollin policy} \; \pi^{in} = \beta\pi^{\star} + (1-\beta)H}\\ & \quad \mathbf{for} \; (\mathbf{x},\mathbf{y}) \in D_{train} \; \mathbf{do}\\ & \quad \quad \color{red}{\text{generate trajectory} \; \hat \alpha_1\dots\hat \alpha_T = \pi^{in}(\mathbf{x},\mathbf{y})}\\ & \quad \quad \mathbf{for} \; \hat \alpha_t \in \hat \alpha_1\dots\hat \alpha_T \; \mathbf{do}\\ & \quad \quad \quad \color{red}{\text{ask expert for best action}\; \alpha^{\star} = \pi^{\star}(\mathbf{x},S_{t-1})} \\ & \quad \quad \quad \text{extract features} \; \mathit{feat}=\phi(\mathbf{x},S_{t-1}) \\ & \quad \quad \quad \cal E = \cal E \cup (\mathit{feat},\alpha^{\star})\\ & \quad \text{learn}\; H \; \text{from}\; \cal E\\ & \quad \color{red}{\text{decrease} \; \beta}\\ \end{align}

Proposed by Ross et al. (2011) motivated by robotics

• first iteration is standard classification training
• task loss and gold standard are implicitly considered via the expert
• DAgger: the Datasets in each iteration are Aggregated

rollins expose to previous mistakes. Future ones?

rollouts: expose the classifier to future mistakes!

Training labels as costs

cb_gold

timestep	Pronoun	Modal	Verb	Noun	features
t=1	0	1	1	1	token=I, prev=NULL...
t=2	1	0	1	1	token=can, prev=Pronoun...
t=3	1	1	0	1	token=fly, prev=Modal...

Cost break down

p = gold_path.copy()
cost = 1
cb_costs = []
cb_costs.append(cg.draw_cost_breakdown(rows, columns, [(0,4),(1,3)], roll_in_cell=p[1]))
cb_costs.append(cg.draw_cost_breakdown(rows, columns, [(0,4),(1,3),(2,0)], roll_in_cell=p[1], explore_cell=(2,0)))
cb_costs.append(cg.draw_cost_breakdown(rows, columns, [(0,4),(1,3),(2,0),(3,1)], roll_in_cell=p[1], explore_cell=(2,0),roll_out_cell=(3,0)))
cb_costs.append(cg.draw_cost_breakdown(rows, columns, [(0,4),(1,3),(2,0),(3,1)], cost, p[3], roll_in_cell=p[1], explore_cell=(2,0),roll_out_cell=(3,0)))
for i in range(1,4):
    p = gold_path.copy()
    p[2] = (gold_path[2][0],i)
    if p == gold_path:
        cost = 0
    else:
        cost = 1
    cb_costs.append(cg.draw_cost_breakdown(rows, columns, p, cost, p[3], roll_in_cell=p[1],roll_out_cell=(3,0), explore_cell=p[2]))
util.Carousel(cb_costs)

Previous   Next

</tr> </thead>

</tr> </tbody> </table>

• rollin to a point in the sentence
• explore each action: rollout and cost with task loss

Mixed rollouts

cb_mix_costs = []
cb_mix_costs.append(cg.draw_cost_breakdown(rows, columns, [(0,4),(1,3)], roll_in_cell=p[1]))
cb_mix_costs.append(cg.draw_cost_breakdown(rows, columns, [(0,4),(1,3),(2,0)], roll_in_cell=p[1], explore_cell=(2,0)))
for i in range(4):
    p = gold_path.copy()
    p[2] = (gold_path[2][0],i)
    if p == gold_path:
        cost = 0
    elif i==1:
        cost =2
        p[3] = (3,0)
    else:
        cost = 1
    cb_mix_costs.append(cg.draw_cost_breakdown(rows, columns, p, cost, p[3], roll_in_cell=p[1],roll_out_cell=(3,0), explore_cell=p[2]))
util.Carousel(cb_mix_costs)

Previous   Next

step	Pronoun	Modal	Verb	Noun	features
t=2	1	0	1	1	token=can, prev=Pronoun...

Pronoun	Modal	Verb	Noun	features
1	0	2	1	token=can, prev=Pronoun...

**Mixed rollout** with the expert $\pi^{\star}$ and the classifier $H$: $$\pi^{out} = \beta\pi^{\star} + (1-\beta)H$$

DAgger with roll-outs

\begin{align} & \textbf{Input:} \; D_{train} = \{(\mathbf{x}^1,\mathbf{y}^1)...(\mathbf{x}^M,\mathbf{y}^M)\}, \; \text{expert}\; \pi^{\star}, \; \text{classifier} \; H, \; \text{loss} \; L\\ & \text{set training examples}\; \cal E = \emptyset, \; \pi^{\star}\; \mathrm{probability}\; \beta=1\\ & \mathbf{while}\; \text{termination condition not reached}\; \mathbf{do}\\ & \quad \color{red}{\text{set rollin/out policy} \; \pi^{in/out} = \beta\pi^{\star} + (1-\beta)H}\\ & \quad \mathbf{for} \; (\mathbf{x},\mathbf{y}) \in D_{train} \; \mathbf{do}\\ & \quad \quad \text{rollin to predict} \; \hat \alpha_1\dots\hat \alpha_T = \pi^{in/out}(\mathbf{x},\mathbf{y})\\ & \quad \quad \mathbf{for} \; \hat \alpha_t \in \hat \alpha_1\dots\hat \alpha_T \; \mathbf{do}\\ & \quad \quad \quad \mathbf{for} \; \alpha \in {\cal A} \; \mathbf{do}\\ & \quad \quad \quad \quad \color{red}{\text{rollout} \; S_{final} = \pi^{in/out}(S_{t-1}, \alpha, \mathbf{x})}\\ & \quad \quad \quad \quad \color{red}{\text{cost}\; c_{\alpha}=L(S_{final}, \mathbf{y})}\\ & \quad \quad \quad \text{extract features}\; \mathit{feat}=\phi(\mathbf{x}, S_{t-1}) \\ & \quad \quad \quad \cal E = \cal E \cup (\mathit{feat},\mathbf{c})\\ & \quad \text{learn} \;H \; \text{from}\; \cal E\\ & \quad \text{decrease} \; \beta\\ \end{align}

Roll-outs

• can learn with sub-optimal experts
• expensive when there are many actions and long sequences to complete outputs

• first proposed in SEARN (Daumé III et al., 2009)

• used to hybridise DAgger by Vlachos and Clark (2014), referred to later as V-DAgger (Goodman et al. 2016)

• also proposed as look-aheads (Tsuruoka et al. 2011)

LoLS

Locally Optimal Learning to Search (Chang et al., 2015)

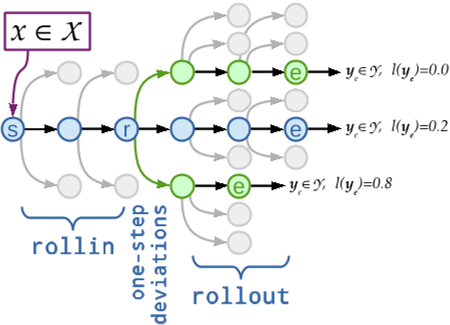
• rollin always with the classifier
• each rollout uses only the expert or the classifier

Generic imitation learning

\begin{align} & \textbf{Input:} \; D_{train} = \{(\mathbf{x}^1,\mathbf{y}^1)...(\mathbf{x}^M,\mathbf{y}^M)\}, \; \text{expert}\; \pi^{\star}, \text{classifier} \; H, \; \text{loss} \; L\\ & \text{set training examples}\; \cal E = \emptyset\\ & \mathbf{while}\; \text{termination condition not reached}\; \mathbf{do}\\ & \quad \color{red}{\text{set rollin policy} \; \pi^{in} = mix(H,\pi^{\star})}\\ & \quad \color{red}{\text{set rollout policy} \; \pi^{out} = mix(H,\pi^{\star})}\\ & \quad \mathbf{for} \; (\mathbf{x},\mathbf{y}) \in D_{train} \; \mathbf{do}\\ & \quad \quad \color{red}{\text{rollin to predict} \; \hat \alpha_1\dots\hat \alpha_T = \pi^{in}(\mathbf{x},\mathbf{y})}\\ & \quad \quad \mathbf{for} \; \hat \alpha_t \in \hat \alpha_1\dots\hat \alpha_T \; \mathbf{do}\\ & \quad \quad \quad \color{red}{\text{rollout to obtain costs}\; c \; \text{for all possible actions using}\; L}\\ & \quad \quad \quad \text{extract features}\; \mathit{feat}=\phi(\mathbf{x},S_{t-1}) \\ & \quad \quad \quad \cal E = \cal E \cup (\mathit{feat},c)\\ & \quad \text{learn}\; H \; \text{from}\; \cal E\\ \end{align}

Overview

Method	rollin	rollout	loss	expert decay	training data
classification	expert	N/A	0/1	N/A	single iteration
DAgger	mix	N/A	0/1	decrease	all iterations
V-DAgger	mix	mix	task	exponential	all iterations
LOLS	classifier	action-level mix	task	no decay	averaged across iterations
SEARN	mix	mix	task	exponential	weighted averaged across iterations

Summary so far

• basic intuition behind IL
• rollin and the DAgger algorithm
• rollouts, V-DAgger and LOLS
• generic imitation learning recipe