First part recap

Imitation Learning

Meta-learning for action-based models:
improve classifier by generating training from demonstrations

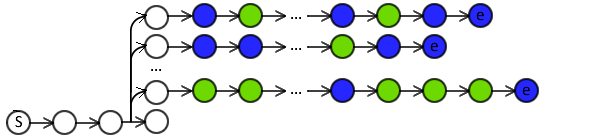
Rollin

For each training instance:

  • construct an action sequence,
  • incrementally transform initial to terminal state.
  • Available actions wrt transition system.

Rollin

For each training instance:

  • construct an action sequence,
  • incrementally transform initial to terminal state.
  • Available actions wrt transition system.

Rollin

Can rollin with classifier, expert policy, or a mix.

Explore

At each timestep:

  • explore alternative actions w.r.t transition system.

Explore

Create a new training instance (feature vector):

  • cost alternative actions,
  • e.g. DAgger

Rollout

Or perform rollouts to cost the actions:

  • can use non-decomposable loss functions,
  • e.g. V-DAgger, SEARN, LOLS

Rollout

Can rollout with classifier, expert policy, or a mix.

Part 2: NLP Applications and practical advice

  • Applications:
    • dependency parsing
    • natural language generation
    • semantic parsing
  • Practical advice
    • making things faster
    • debugging

Applying Imitation Learning to Dependency Parsing

[Goldberg and Nivre 2012](http://www.aclweb.org/anthology/C12-1059)

Dependency parsing

To represent the syntax of a sentence as directed labeled arcs between words.

  • Labels represent dependencies between words.

DAgger Reminder

\begin{align} & \textbf{Input:} \; D_{train} = \{(\mathbf{x}^1,\mathbf{y}^1)...(\mathbf{x}^M,\mathbf{y}^M)\}, \; \text{expert}\; \pi^{\star}, \; \text{classifier} \; H\\ & \text{set training examples}\; \cal E = \emptyset ,\; \color{red}{\pi^{\star}\; \mathrm{probability}\; \beta=1}\\ & \mathbf{while}\; \text{termination condition not reached}\; \mathbf{do}\\ & \quad \color{red}{\text{set rollin policy} \; \pi^{in} = \beta\pi^{\star} + (1-\beta)H}\\ & \quad \mathbf{for} \; (\mathbf{x},\mathbf{y}) \in D_{train} \; \mathbf{do}\\ & \quad \quad \color{red}{\text{generate trajectory} \; \hat \alpha_1\dots\hat \alpha_T = \pi^{in}(\mathbf{x},\mathbf{y})}\\ & \quad \quad \mathbf{for} \; \hat \alpha_t \in \hat \alpha_1\dots\hat \alpha_T \; \mathbf{do}\\ & \quad \quad \quad \color{red}{\text{ask expert for } \underline{\text{a set of best actions}}\; \{\alpha_{1}^{\star}\dots\alpha_{k}^{\star}\} = \pi^{\star}(\mathbf{x},S_{t-1})} \\ & \quad \quad \quad \text{extract features} \; \mathit{feat}=\phi(\mathbf{x},S_{t-1}) \\ & \quad \quad \quad \cal E = \cal E \cup (\mathit{feat},\alpha^{\star})\\ & \quad \text{learn}\; H \; \text{from}\; \cal E\\ & \quad \color{red}{\text{decrease} \; \beta}\\ \end{align}

To apply Imitation Learning on any task, we need to define:

  • Transition
  • Loss function
  • Expert policy

Transition system?

We can assume any transition-based system (e.g. Arc-Eager).

State: arcs, stack, and buffer.

Action space:
Shift, Reduce, Arc-Left, and Arc-Right.</span>

  • Arc-Left / Arc-Right combine with arc labels,
  • but limited #labels in dependency parsing (~50).

The length of the transition sequence is variable.


Shift -> Shift -> Arc-Right -> Shift -> ... -> Arc-Left

  • Bounded (but not fixed) by length of sentence.
  • In what task would it be fixed? POS tagging!

...



Stack: -
Buffer: ROOT, 'economic', 'news', 'had', 'little', 'effect', 'on', 'financial', 'markets', '.'

Shift



Stack: ROOT
Buffer: 'economic', 'news', 'had', 'little', 'effect', 'on', 'financial', 'markets', '.' </font>

Shift



Stack: ROOT, 'economic'
Buffer: 'news', 'had', 'little', 'effect', 'on', 'financial', 'markets', '.' </font>

Arc-Left: amod



Stack: ROOT
Buffer: 'news', 'had', 'little', 'effect', 'on', 'financial', 'markets', '.'

Shift



Stack: ROOT, 'news'
Buffer: 'had', 'little', 'effect', 'on', 'financial', 'markets', '.' </font>

Arc-Left: nsubj



Stack: ROOT
Buffer: 'had', 'little', 'effect', 'on', 'financial', 'markets', '.'

and so on



Stack: ROOT
Buffer: -

Loss function?

Hamming loss: given predicted arcs, how many parents and labels were incorrectly predicted?

  • Directly corresponds to attachment score metrics used to evaluate dependency parsers.
  • Costs dependencies, not actions directly.
  • Decomposable? Not with this transition model! Cannot score Shift independent of Arc-Right!

Expert policy?

Returns the best action at the current state by looking at the gold standard assuming future actions are also optimal:

$$\alpha^{\star}=\pi^{\star}(S_t, \mathbf{y}) = \mathop{\arg \min}_{\alpha \in {\cal A}} L(S_t(\alpha,\pi^{\star}),\mathbf{y})$$

How do we make an expert policy?

We can derive a static transition sequence from initial to terminal state using the golden standard.

  • Static expert policy.

Static expert does not take previous actions into account.

Static expert has not encountered this state before.

  • Cannot know which is the optimal action.
  • May default to an action (e.g. Shift).

A static expert may be sufficient for tasks where we do not care whether the previous actions were optimal.

  • What would such a task be? POS tagging.

Rollin mistakes in dependency parsing

Let's assume that we rollin using the classifier.

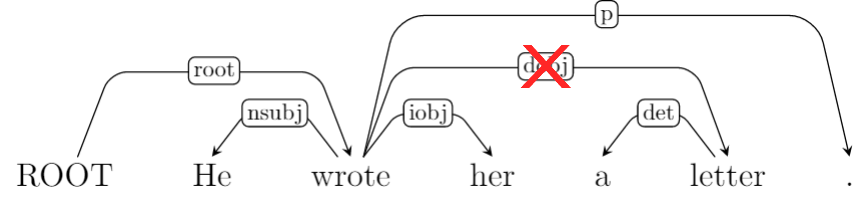
Arc-Right: iobj ?



Stack: 'wrote'
Buffer: 'her', 'a', 'letter', '.'

Shift



Stack: 'wrote', 'her'
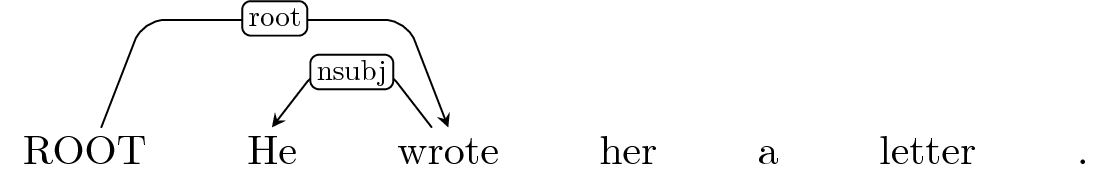
Buffer: 'a', 'letter', '.' </font>

Default: Shift



Stack: 'wrote', 'her', 'a'
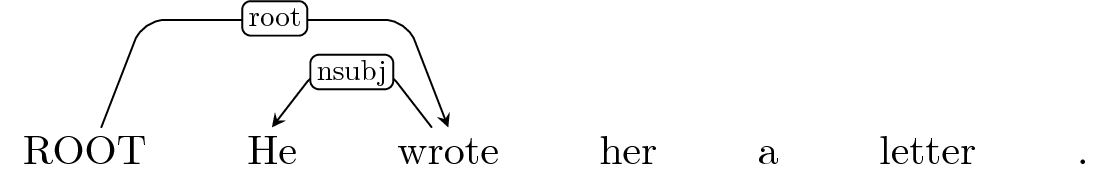
Buffer: 'letter', '.' </font>

Arc-Left: det



Stack: 'wrote', 'her'
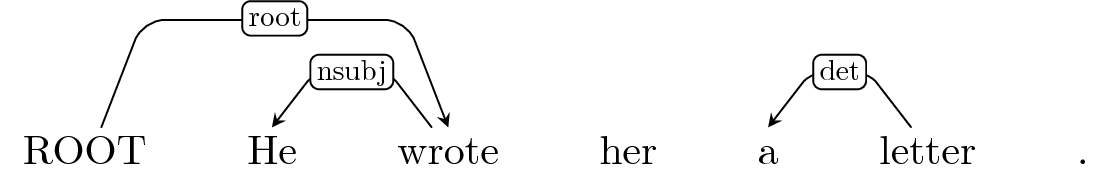
Buffer: 'letter', '.'

Default: Shift



Stack: 'wrote', 'her', 'letter'
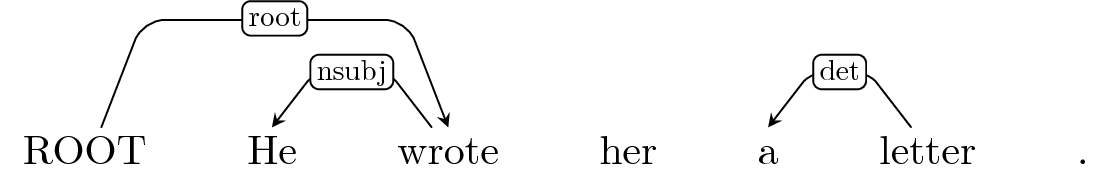
Buffer: '.' </font>



Default: Shift



Stack: 'wrote', 'her', 'letter', '.'
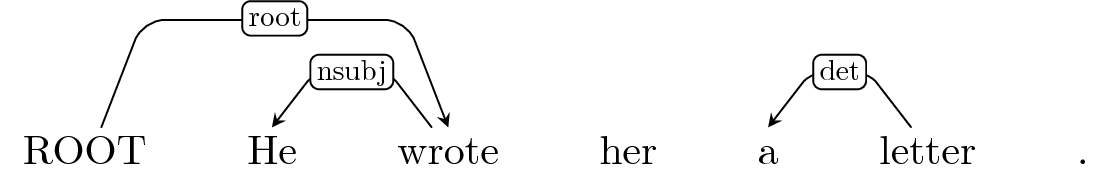
Buffer: - </font>

Static expert policy cannot recover from errors in the rollin.

Also, what if there are multiple correct transitions?

Stack: 'her'
Buffer: 'a', 'letter', '.'

Two possible actions: Reduce 'her' / Shift 'a'

Static expert policy arbitarilly choses.

  • But chosing any one action indirectly labels the alternative actions as incorrect!
  • Leads to noise in the training signal.

Dynamic expert policy

Determines best action, by considering the previous actions.

  • Can recover from errors.
  • Allows for multiple optimal actions at each time-step.

Reachable terminal state

Reachable terminal state:

  • Can be reached through a sequence of expert actions $\alpha_1^{\star}\dots \alpha_T^{\star}$, and
  • no further actions can be taken at that state.
  • For an optimal reachable terminal state, $L(S_{final}, \mathbf{y}) = 0$.

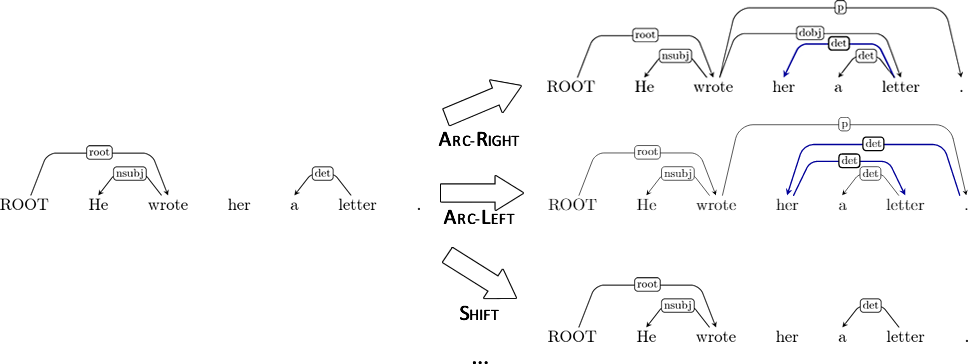
How does a dynamic expert policy work?

For each possible action at a time-step:

  • ...

...

Stack: 'wrote', 'her'
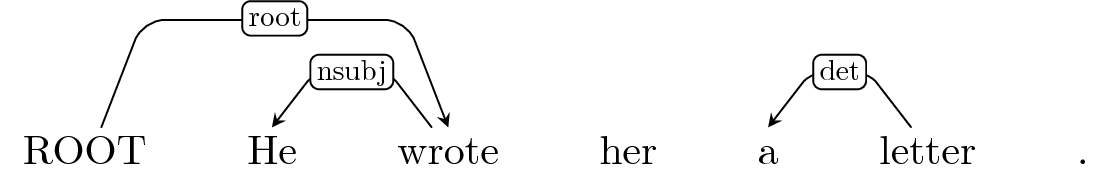
Buffer: 'letter', '.'

How does a dynamic expert policy work?

For each possible action at a time-step:

  • Arc-Left? Arc-Right? Reduce? Shift?

Stack: 'wrote', 'her'
Buffer: 'letter', '.'

How does a dynamic expert policy work?

For each possible action at a time-step:

  • Arc-Left? Arc-Right? Reduce? Shift?

  • Determine the reachable terminal state.

  • Use full rollout with expert?





Arc-Left: det?



Stack: 'wrote',
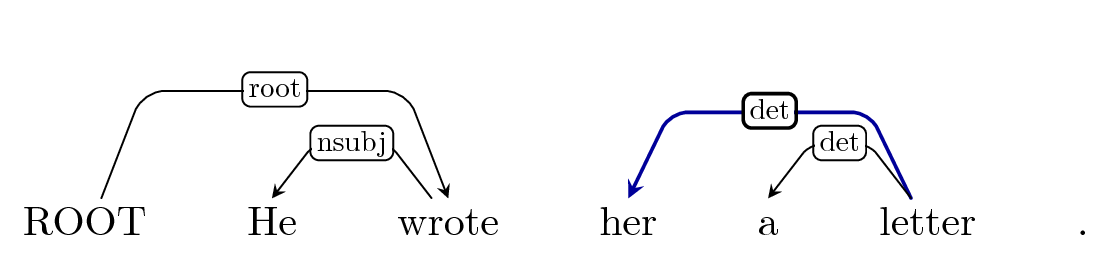
Buffer: 'letter', '.'

Arc-Right: dobj



Stack: 'wrote',
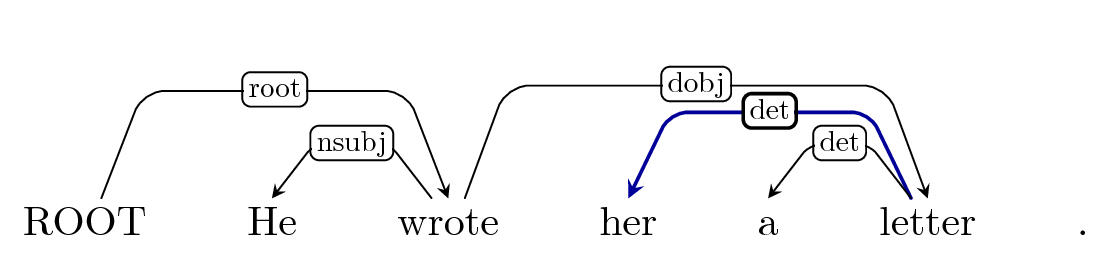
Buffer: '.'

Arc-Right: p



Stack: 'wrote',
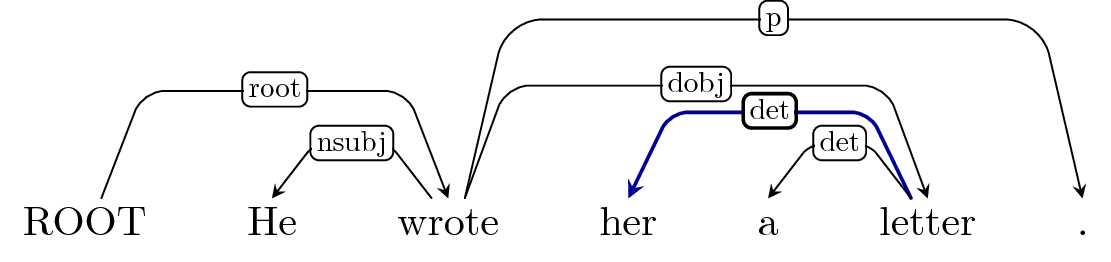
Buffer: -

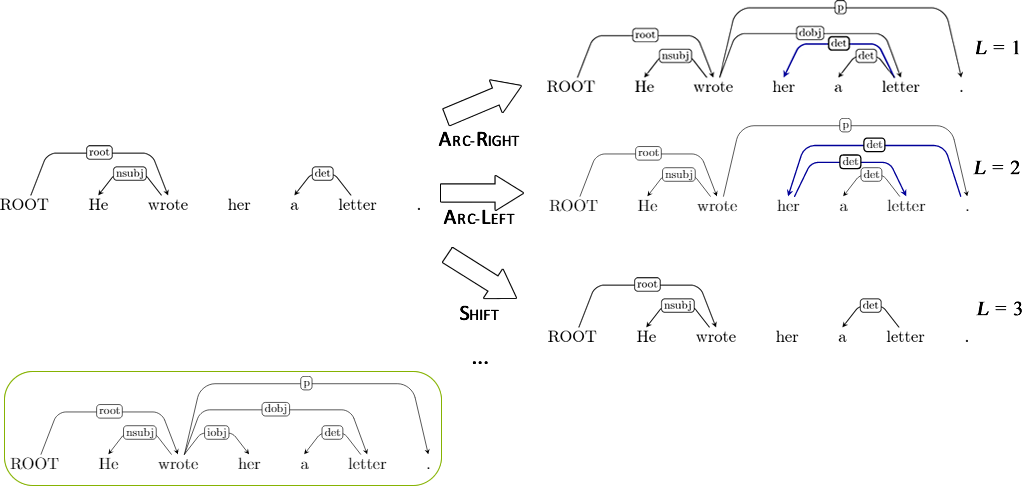
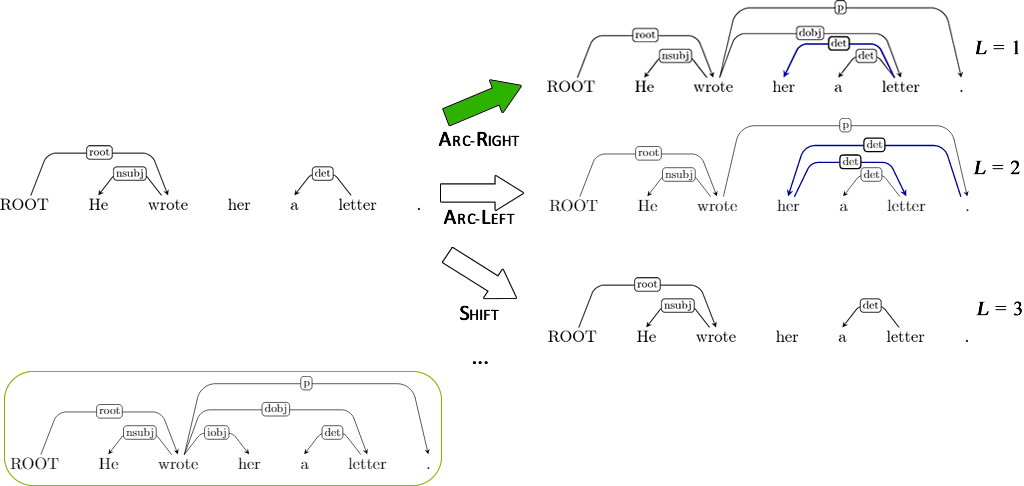
Full rollouts may be expensive

Instead of full expert rollout, we may use heuristics!

  • i.e. can we estimate how an action will effect the reachable terminal state?

Arc-Right: det?

Stack: 'wrote', 'her'
Buffer: '.'

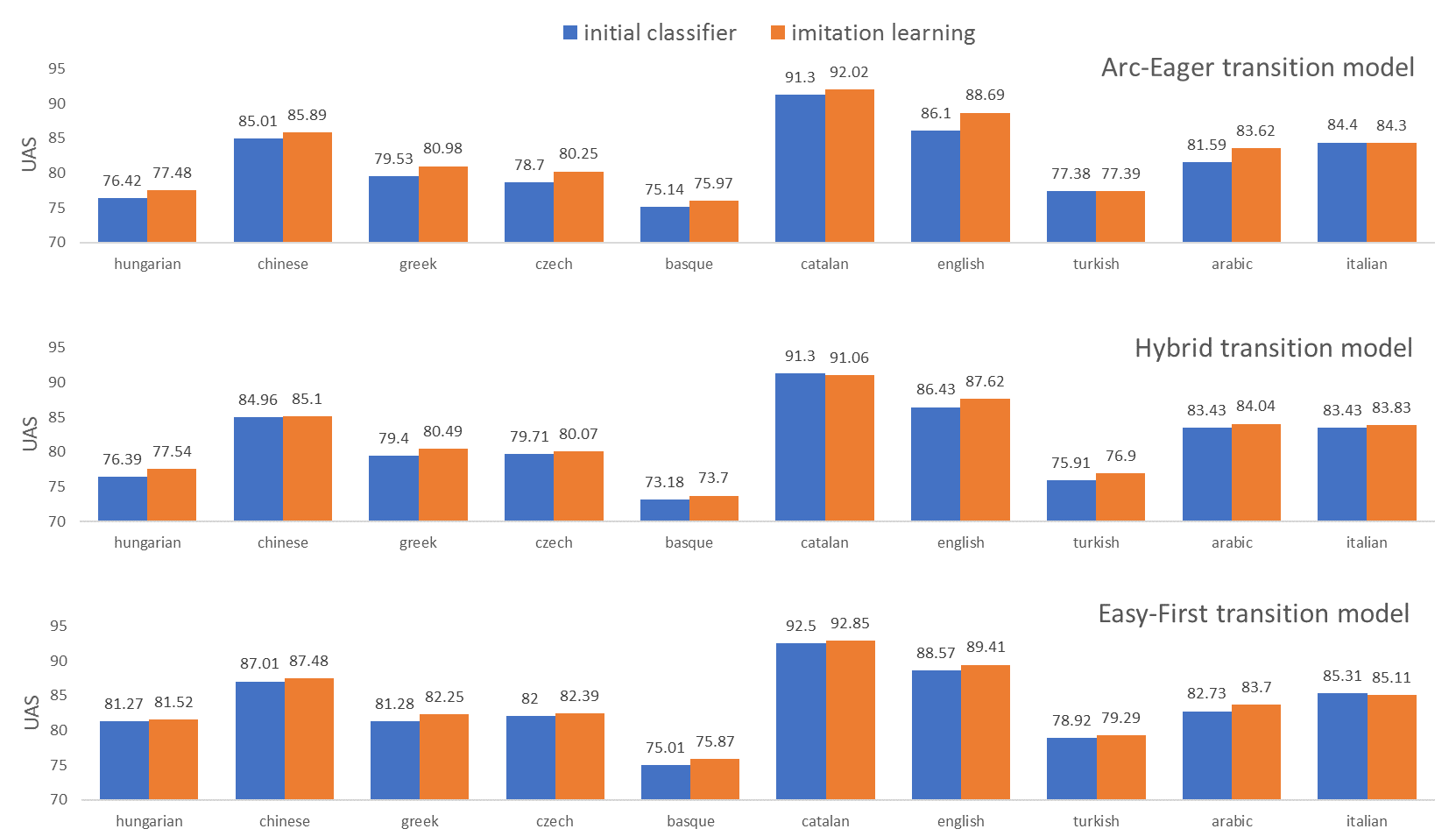
Results

[Goldberg and Nivre 2012](http://www.aclweb.org/anthology/C12-1059)