Applying Imitation Learning on Natural Language Generation
[Lampouras and Vlachos 2016](https://aclweb.org/anthology/C/C16/C16-1105.pdf)
Natural Language Generation (concept-to-text)¶
The natural language processing task of generating text from a meaning representation.
\begin{align} & \text{Predicate: INFORM}\\ & \text{______________________}\\ & \color{blue}{\text{type = "hotel"}}\\ & \color{green}{\text{count = "182"}}\\ & \color{red}{\text{dogs_allowed = dont_care}} \end{align}
There are 182 hotels if you do not care whether dogs are allowed.
Transition system?¶
State: meaning representation, incomplete sentence.
Action space:
- What to say?: content prediction actions ac, and
- How to say it?: word prediction actions aw .
...

\begin{align} & \text{Predicate: INFORM}\\ & \text{______________________}\\ & \text{name = X-name-1}\\ & \text{serves = food}\\ & \text{eattype = restaurant}\\ & \text{near = riverside}\\ & \text{area = X-area-1, X-area-2} \end{align}
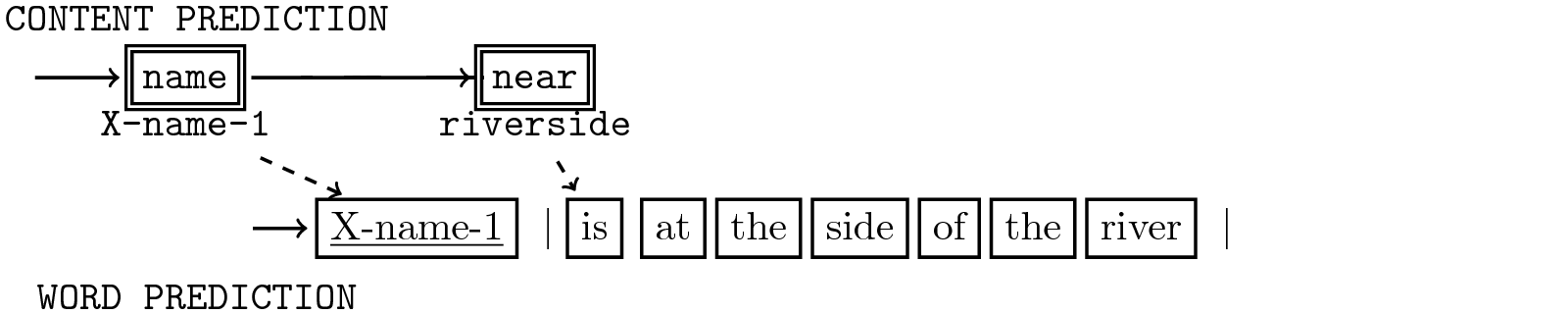
Content: name

\begin{align} & \text{Predicate: INFORM}\\ & \text{______________________}\\ & \color{red}{\textbf{name}} \text{ = X-name-1}\\ & \text{serves = food}\\ & \text{eattype = restaurant}\\ & \text{near = riverside}\\ & \text{area = X-area-1, X-area-2} \end{align}
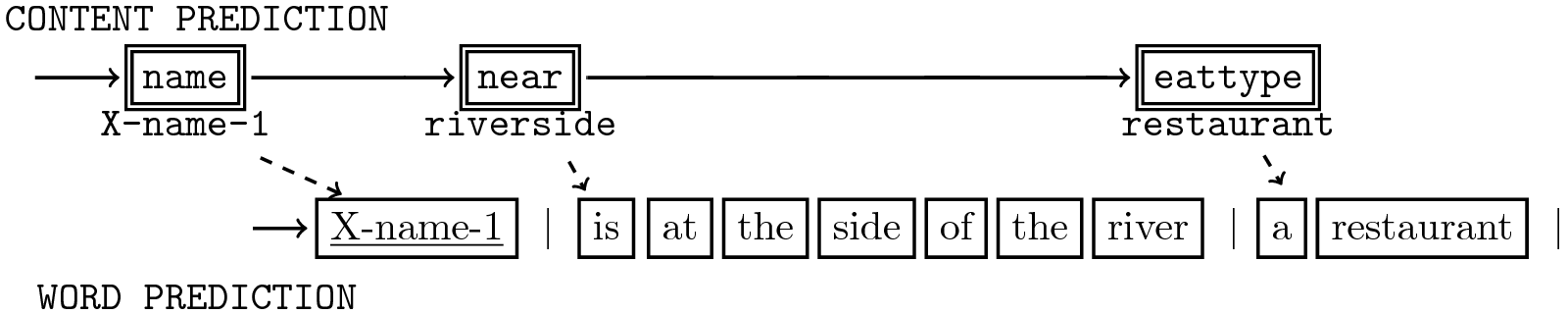
Content: eattype

\begin{align} & \text{Predicate: INFORM}\\ & \text{______________________}\\ & \color{red}{\textbf{name}}\text{ = X-name-1}\\ & \text{serves = food}\\ & \color{red}{\textbf{eattype}}\text{ = restaurant}\\ & \text{near = riverside}\\ & \text{area = X-area-1, X-area-2} \end{align}
and so on

\begin{align} & \text{Predicate: INFORM}\\ & \text{______________________}\\ & \color{red}{\textbf{name}}\text{ = X-name-1}\\ & \text{serves = food}\\ & \color{red}{\textbf{eattype}}\text{ = restaurant}\\ & \color{red}{\textbf{near}}\text{ = riverside}\\ & \color{red}{\textbf{area}}\text{ = X-area-1, X-area-2} \end{align}
Word: X-name-1

\begin{align} & \text{Predicate: INFORM}\\ & \text{______________________}\\ & \color{red}{\textbf{name = X-name-1}}\\ & \text{serves = food}\\ & \color{red}{\textbf{eattype}}\text{ = restaurant}\\ & \color{red}{\textbf{near}}\text{ = riverside}\\ & \color{red}{\textbf{area}}\text{ = X-area-1, X-area-2} \end{align}
Word: EoS

\begin{align} & \text{Predicate: INFORM}\\ & \text{______________________}\\ & \color{red}{\textbf{name = X-name-1}}\\ & \text{serves = food}\\ & \color{red}{\textbf{eattype}}\text{ = restaurant}\\ & \color{red}{\textbf{near}}\text{ = riverside}\\ & \color{red}{\textbf{area}}\text{ = X-area-1, X-area-2} \end{align}
Word: is

\begin{align} & \text{Predicate: INFORM}\\ & \text{______________________}\\ & \color{red}{\textbf{name = X-name-1}}\\ & \text{serves = food}\\ & \color{red}{\textbf{eattype}}\text{ = restaurant}\\ & \color{red}{\textbf{near}}\text{ = riverside}\\ & \color{red}{\textbf{area}}\text{ = X-area-1, X-area-2} \end{align}
Word: a

\begin{align} & \text{Predicate: INFORM}\\ & \text{______________________}\\ & \color{red}{\textbf{name = X-name-1}}\\ & \text{serves = food}\\ & \color{red}{\textbf{eattype}}\text{ = restaurant}\\ & \color{red}{\textbf{near}}\text{ = riverside}\\ & \color{red}{\textbf{area}}\text{ = X-area-1, X-area-2} \end{align}
Word: restaurant

\begin{align} & \text{Predicate: INFORM}\\ & \text{______________________}\\ & \color{red}{\textbf{name = X-name-1}}\\ & \text{serves = food}\\ & \color{red}{\textbf{eattype = restaurant}}\\ & \color{red}{\textbf{near}}\text{ = riverside}\\ & \color{red}{\textbf{area}}\text{ = X-area-1, X-area-2} \end{align}
Word: EoS

\begin{align} & \text{Predicate: INFORM}\\ & \text{______________________}\\ & \color{red}{\textbf{name = X-name-1}}\\ & \text{serves = food}\\ & \color{red}{\textbf{eattype = restaurant}}\\ & \color{red}{\textbf{near}}\text{ = riverside}\\ & \color{red}{\textbf{area}}\text{ = X-area-1, X-area-2} \end{align}
and so on

\begin{align} & \text{Predicate: INFORM}\\ & \text{______________________}\\ & \color{red}{\textbf{name = X-name-1}}\\ & \text{serves = food}\\ & \color{red}{\textbf{eattype = restaurant}}\\ & \color{red}{\textbf{near = riverside}}\\ & \color{red}{\textbf{area = X-area-1, X-area-2}} \end{align}
Word actions are chosen based on content actions.
- Content actions precede word actions.
- The length of the transition sequence is variable.
- Instead, alternate between content and word actions?

Different classifiers are required for content and word actions.
- Actually, a different word classifier per content action.
- Doesn't affect imitation learning!
Action space:
- Content actions limited by the MR.
- Word actions limited to gold standard observations.
Loss function?¶
BLEU: % of n-grams predicted present in the gold standard,
i.e. $L=1-BLEU(s_{final}, \mathbf{y})$</span></li>
Same as NLG's evaluation metric.
Content actions are ignored by loss function.
- Indirectly costed by their impact on word actions.
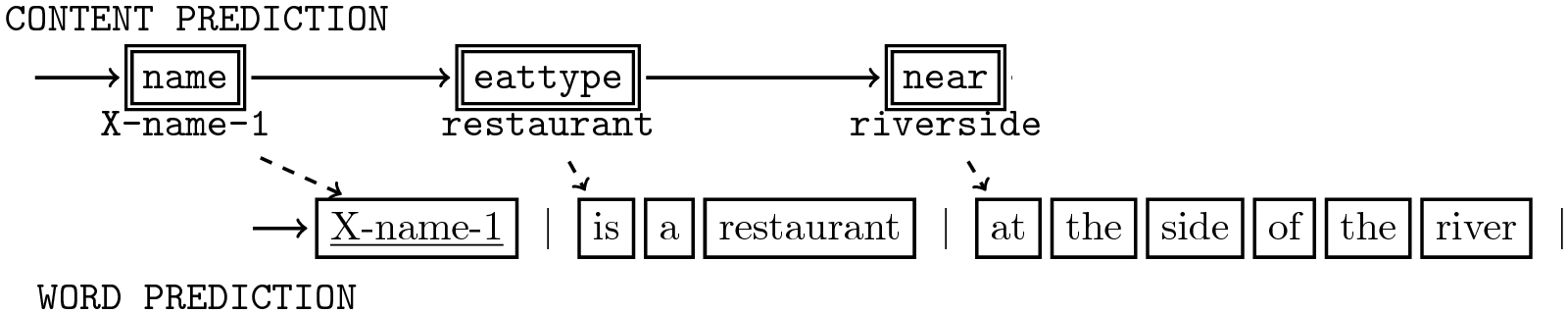
No explicit supervision on how each word is aligned to which attribute.
- Evaluate how good the complete final sentence is.


The loss function also penalizes undesirable behaviour:
- Repeating the same word,
- predicting content not present in the MR,
- etc.
Expert policy?¶
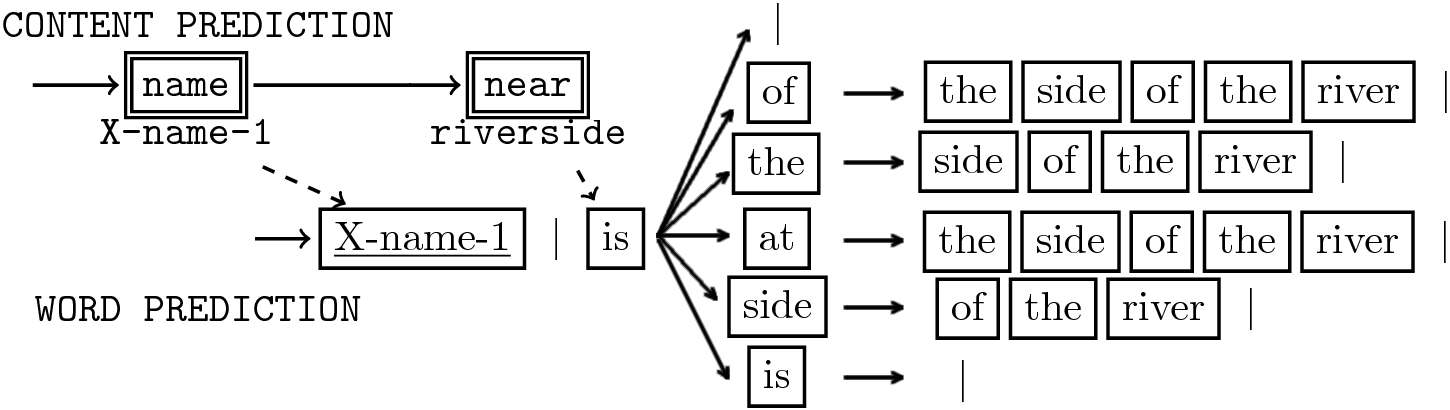
For word actions:
- Which word makes the sequence best match the gold standard.
- Only consider words in gold standard.
- Best match = minimize loss function.
If content actions:
- which content actions to include,
- and in what order.
Need alignments between MR and words in gold standard.
- Loss requires no explicit supervision on alignments.
- Can employ heuristics on the gold standard!
\begin{align} & \text{Predicate: INFORM}\\ & \text{______________________}\\ & \color{blue}{\text{type = "hotel"}}\\ & \color{green}{\text{count = "182"}}\\ & \color{red}{\text{dogs_allowed = dont_care}} \end{align}
There are 182 hotels if you do not care whether dogs are allowed.
Suboptimal expert policy¶
The expert policy depends on naive heuristics.
- mistakes happen...
\begin{align} & \text{Predicate: INFORM}\\ & \text{______________________}\\ & \color{blue}{\text{type = "hotel"}}\\ & \color{green}{\text{count = "182"}}\\ & \color{red}{\text{dogs_allowed = false}} \end{align}
There are 182 hotels if you are traveling without animals.
Dealing with suboptimal¶
Imitating the suboptimal expert policy is not enough.
- Should not rely heavily on expert policy during rollin/rollouts.
- e.g. DAgger uses expert exclusively to cost actions.
We need to learn a better classifier than the suboptimal expert.
- Use rollouts that mix classifier and expert policy.
- We will be using LOLS here.
Locally Optimal Learning to Search
\begin{align} & \textbf{Input:} \; D_{train} = \{(\mathbf{x}^1,\mathbf{y}^1)...(\mathbf{x}^M,\mathbf{y}^M)\}, \; expert\; \pi^{\star}, \; loss \; function \; L\\ & \text{set} \; training\; examples\; \cal E = \emptyset\\ & \color{red}{\text{initialize a classifier } H_{0}}\\ & \mathbf{for}\; i = 0 \;\mathbf{to} \; N\; \mathbf{do}\\ & \quad \color{red}{\text{set} \; rollin \; policy \; \pi^{in} = H_i}\\ & \quad \color{red}{\text{set} \; rollout \; policy \; \pi^{out} = mix(H_i,\pi^{\star})}\\ & \quad \mathbf{for} \; (\mathbf{x},\mathbf{y}) \in D_{train} \; \mathbf{do}\\ & \quad \quad \text{rollin to predict} \; \hat \alpha_1\dots\hat \alpha_T = \pi^{in}(\mathbf{x},\mathbf{y})\\ & \quad \quad \mathbf{for} \; \hat \alpha_t \in \hat \alpha_1\dots\hat \alpha_T \; \mathbf{do}\\ & \quad \quad \quad \text{rollout to obtain costs}\; c \; \text{for all possible actions using}\; L\; \\ & \quad \quad \quad \text{extract features}\; f=\phi(\mathbf{x},S_{t-1}) \\ & \quad \quad \quad \cal E = \cal E \cup (f,c)\\ & \quad \color{red}{\text{learn classifier} \; H_{i+1} \; \text{from}\; \cal E}\\ & \color{red}{H = \; \mathbf{avg}\{H_{0}\mathbf{\dots}H_{N}\}}\\ \end{align}
Performing the rollin¶

\begin{align} & \text{Predicate: INFORM}\\ & \text{______________________}\\ & \text{name = X-name-1}\\ & \text{eattype = restaurant}\\ & \text{food = chinese} \end{align}
Performing the rollin¶

\begin{align} & \text{Predicate: INFORM}\\ & \text{______________________}\\ & \text{name = X-name-1}\\ & \text{eattype = restaurant}\\ & \text{food = chinese} \end{align}
Explore actions¶

\begin{align} & \text{Predicate: INFORM}\\ & \text{______________________}\\ & \text{name = X-name-1}\\ & \text{eattype = restaurant}\\ & \text{food = chinese} \end{align}
Explore actions¶

\begin{align} & \text{Predicate: INFORM}\\ & \text{______________________}\\ & \text{name = X-name-1}\\ & \text{eattype = restaurant}\\ & \text{food = chinese} \end{align}
Performing the rollout¶

\begin{align} & \text{Predicate: INFORM}\\ & \text{______________________}\\ & \text{name = X-name-1}\\ & \text{eattype = restaurant}\\ & \text{food = chinese} \end{align}
Performing the rollout¶

\begin{align} & \text{Predicate: INFORM}\\ & \text{______________________}\\ & \text{name = X-name-1}\\ & \text{eattype = restaurant}\\ & \text{food = chinese} \end{align}
Performing the rollout¶

\begin{align} & \text{Predicate: INFORM}\\ & \text{______________________}\\ & \text{name = X-name-1}\\ & \text{eattype = restaurant}\\ & \text{food = chinese} \end{align}
Performing the rollout¶

\begin{align} & \text{Predicate: INFORM}\\ & \text{______________________}\\ & \text{name = X-name-1}\\ & \text{eattype = restaurant}\\ & \text{food = chinese} \end{align}
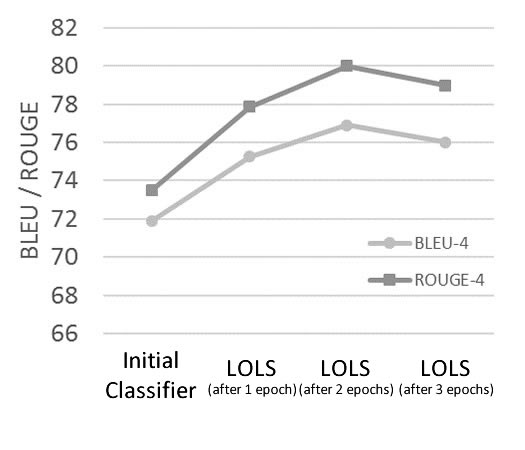
LOLS modifications¶
Exponential decay schedule
Introduced in SEARN (Daumé III et al., 2009)
- Gradual move away from the (suboptimal) expert.
- The costs are adjusted to the classifiers' predictions, thus teaching them to predict actions jointly.
LOLS uses the same policy throughout each rollout.
- But potentially a different policy for each examined action at the same time-step.
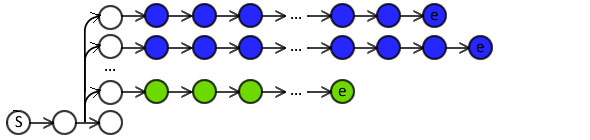
- Here, we also use the same policy for all actions at the same time-step.
Rollin noise¶
Rollin with the classifiers:
- exposes them to their own actions,
- learn to recover from errors.
But may cause noise in feature vectors of latter time-steps.
- Especially, for tasks that are context-dependent.
Sequence correction¶

\begin{align} & \text{Predicate: INFORM}\\ & \text{______________________}\\ & \text{name = X-name-1}\\ & \text{dogs_allowed = yes} \end{align}
Sequence correction¶

\begin{align} & \text{Predicate: INFORM}\\ & \text{______________________}\\ & \text{name = X-name-1}\\ & \text{dogs_allowed = yes} \end{align}
Sequence correction¶

\begin{align} & \text{Predicate: INFORM}\\ & \text{______________________}\\ & \text{name = X-name-1}\\ & \text{dogs_allowed = yes} \end{align}
After a suboptimal action, we apply sequence correction:
- Correct all already explored time-steps using $\pi^{\star}$.

After a suboptimal action, we apply sequence correction:
- Correct all already explored time-steps using $\pi^{\star}$.
- And re-rollin the rest of the sequence using $H$.

After a suboptimal action, we apply sequence correction:
- Correct all already explored time-steps using $\pi^{\star}$.
- And re-rollin the rest of the sequence using $H$.
- i.e. expose classifier to its actions again.

If suboptimal actions are encountered further in the new sequence, sequence correction may again be performed.
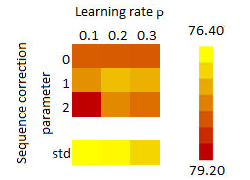
Before sequence correction, allow at most $E$ actions after the suboptimal one.
- i.e. allow the classifiers to learn how to recover from mistakes.
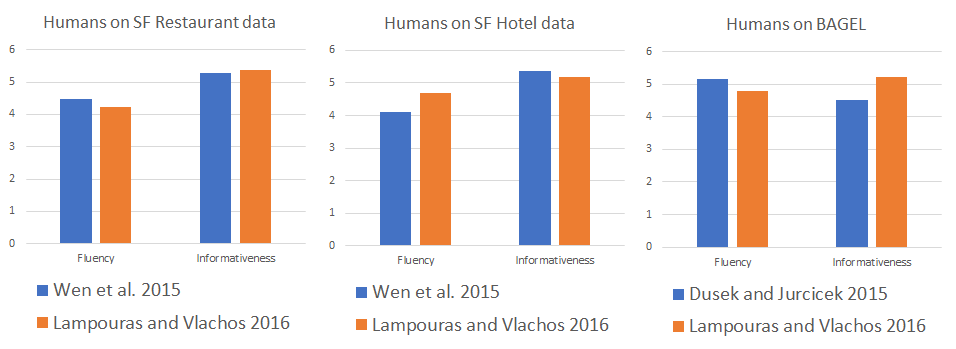
Comparison against state of the art[Lampouras and Vlachos 2016](https://aclweb.org/anthology/C/C16/C16-1105.pdf)
¶