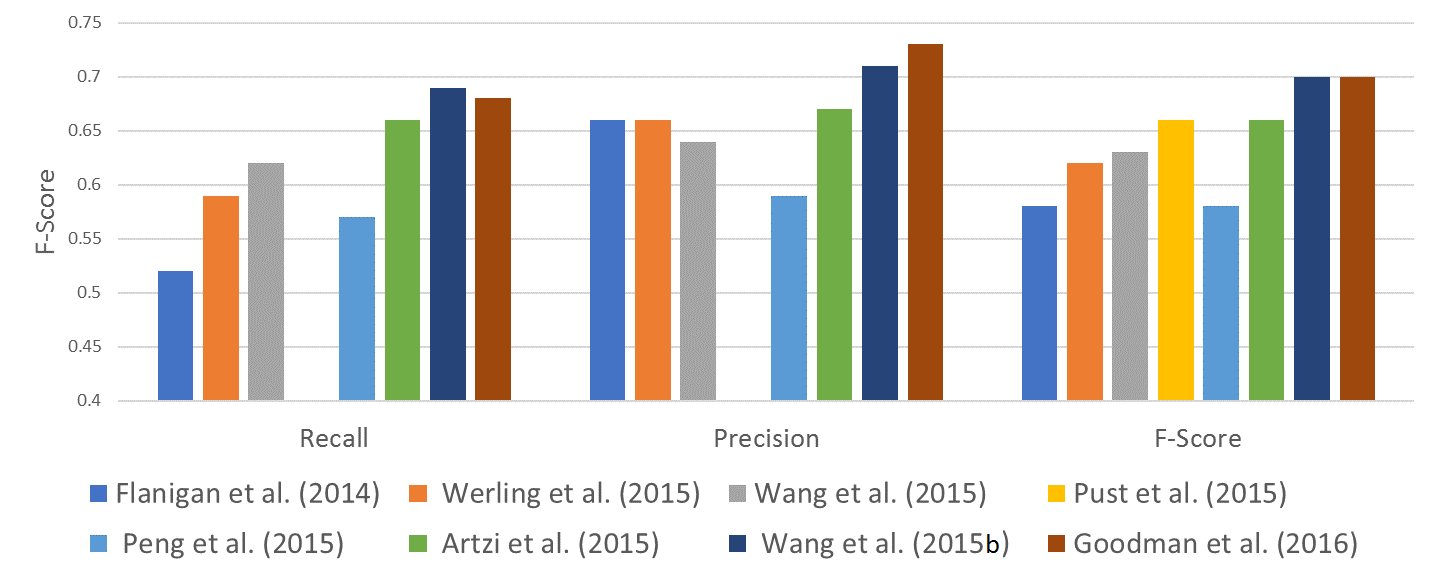
Applying Imitation Learning on Semantic Parsing

[Goodman et al. 2016](http://aclweb.org/anthology/P16-1001)

Semantic parsing

Semantic parsers map natural language to meaning representations.

• Need to abstract over syntactic phenomena,
• resolve anaphora,
• and eliminate ambiguity in language.

• Essentially the inverted task of NLG.

Abstract meaning representation

(Banarescu et al. 2013)

A MR formalism where concept

relations are represented in a DAG.

• Abstracts away from function words, and inflection.


• Transition-based approaches are common.

[AMR tutorial by Schneider et al. 2015](https://github.com/nschneid/amr-tutorial/tree/master/slides)

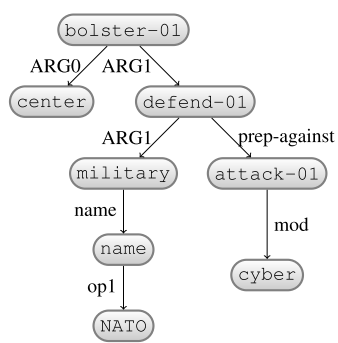
Transition system?

We consider a dependency tree as input.

• Dependency tree is derived from input sentence.

State: nodes, arcs, $\sigma$ and $\beta$ stacks.

• In intermediate states, nodes may be labeled either with words, or AMR concepts.

E

$\sigma$: struck, by, attacks, cyber, in, 2007
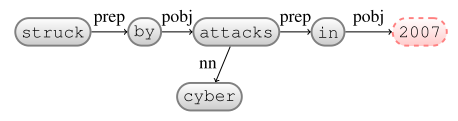
$\beta$: -

Insert: date-entity

$\sigma$: struck, by, attacks, cyber, in, date-entity
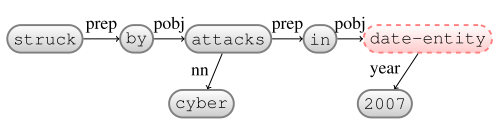
$\beta$: -

ReplaceHead: in

$\sigma$: struck, by, attacks, cyber
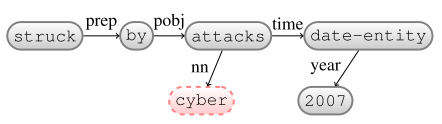
$\beta$: -

Reattach: date-entity

$\sigma$: struck, by, attacks
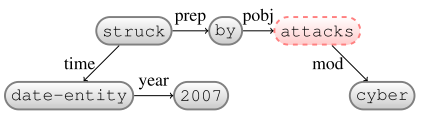
$\beta$: -

ReplaceHead: by

$\sigma$: -
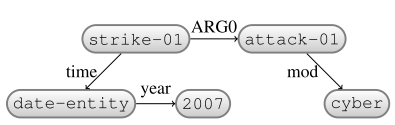
$\beta$: -

Action space

Actions combine with labels

(PropBank framesets).

• #labels in the order of 10³ to 10⁴.
• Performing rollouts for all actions may be time-consuming.

The length of the transition sequence is variable.

• In the range of 50-200 actions.
• Need to prevent cycles between state transitions!

... -> Swap($e_i$, $e_j$) -> Swap($e_j$, $e_i$) -> ...

Also, transition system to preserve acyclicity and

full connectivity in the graph.

Loss function?

Smatch (Cai and Knight, 2013)

• F₁-Score between predicted and gold standard AMR.
• Calculates all possible mappings of nodes.
• Computationally expensive for every rollout
  (NP-complete).

Naive Smatch employs heuristics.

• How many labels and edges in the predicted and gold standard are not present in both?
• Decomposable? No!



• To encourage short sequences,
  a length penalty is applied to the loss.

Expert policy?

A set of heuristic rules, based on alignments between nodes in dependency tree and AMR graph.

• Mapped nodes and edges may need to be renamed.
• Unmapped nodes may need to be inserted or deleted.



• Suboptimal? Yes!

V-DAgger reminder

\begin{align} & \textbf{Input:} \; D_{train} = \{(\mathbf{x}^1,\mathbf{y}^1)...(\mathbf{x}^M,\mathbf{y}^M)\}, \; expert\; \pi^{\star}, \; loss \; function \; L, \\ & \quad \quad \quad learning\; rate\; p\\ & \text{set} \; training\; examples\; \cal E = \emptyset \\ & \mathbf{while}\; \text{termination condition not reached}\; \mathbf{do}\\ & \quad \color{red}{\beta = (1 - p)^i}\\ & \quad \color{red}{\text{set} \; rollin/out \; policy \; \pi^{in/out} = (1-\beta) H + \beta \pi^{\star}}\\ & \quad \mathbf{for} \; (\mathbf{x},\mathbf{y}) \in D_{train} \; \mathbf{do}\\ & \quad \quad \text{rollin to predict} \; \hat \alpha_1\dots\hat \alpha_T = \pi^{in/out}(\mathbf{x},\mathbf{y})\\ & \quad \quad \mathbf{for} \; \hat \alpha_t \in \hat \alpha_1\dots\hat \alpha_T \; \mathbf{do}\\ & \quad \quad \quad \mathbf{for} \; \alpha \in {\cal A} \; \mathbf{do}\\ & \quad \quad \quad \quad \text{rollout} \; S_{final} = \pi^{in/out}(S_{t-1}, \alpha, \mathbf{x})\\ & \quad \quad \quad \quad cost\; c_{\alpha}=L(S_{final}, \mathbf{y})\\ & \quad \quad \quad \text{extract } features=\phi(\mathbf{x}, S_{t-1}) \\ & \quad \quad \quad \cal E = \cal E \cup (features,\mathbf{c})\\ & \quad \text{learn classifier} \; \text{from}\; \cal E\\ \end{align}

Exploration variations

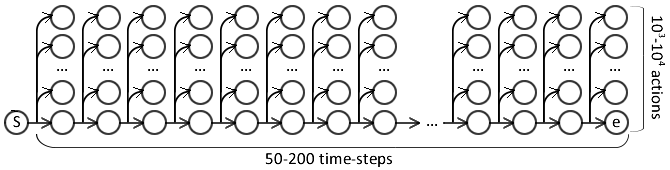
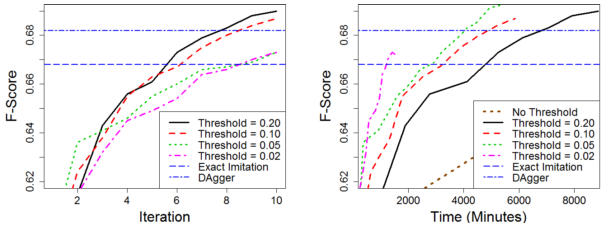
Rollout for 50-200 time-steps, and 10³ to 10⁴ actions.

Partial exploration is used by SCB-LOLS ([Chang et al., 2015](https://arxiv.org/pdf/1502.02206.pdf)).

• Randomly select time-steps and actions to rollout.

Exploration variations

Rollout for 50-200 time-steps, and 10³ to 10⁴ actions.

Targeted exploration is used by [Goodman et al. 2016](http://aclweb.org/anthology/P16-1001):

• Perform rollout only for the expert policy action,
• and actions scored within a threshold $\tau$ from the best.


• In first epoch (no classifier), randomly rollout actions.

Targeted exploration results

[Goodman et al. 2016](http://aclweb.org/anthology/P16-1001)

Step-level stochasticity

V-DAgger and SEARN use step-level mix during roll-out.

• Each rollout step either by classifier or expert.
  
  

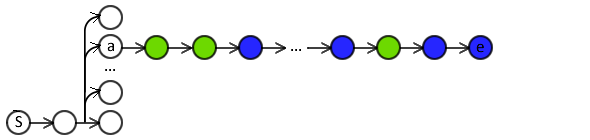
Step-level stochasticity

V-DAgger and SEARN use step-level mix during roll-out.

• Each rollout step either by classifier or expert.
• Rollout on same $a$ may result on different sequence.
  
  

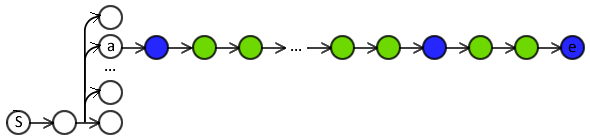
Step-level stochasticity causes high variance in training signal.

• Use LOLS instead?

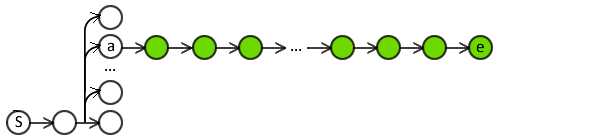
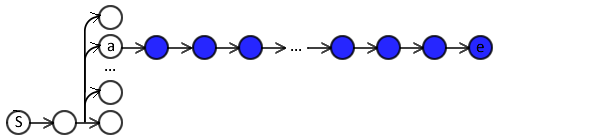
• Sequence too long for full expert policy rollout.

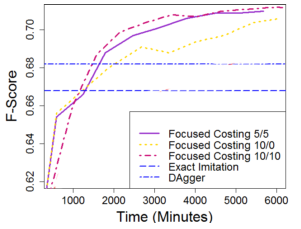
Focused costing

Introduced by Vlachos and Craven, 2011.

• Use the classifier for first $b$ steps of rollout,
• use expert policy for the rest.

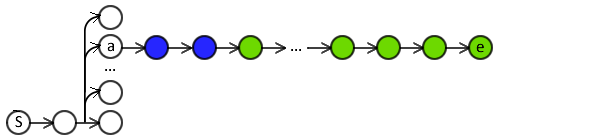
Classifier costing focused on immediate actions.

• No errors in distant actions of the rollout.


• Gradually increase $b$.

Focused costing results

[Goodman et al. 2016](http://aclweb.org/anthology/P16-1001)

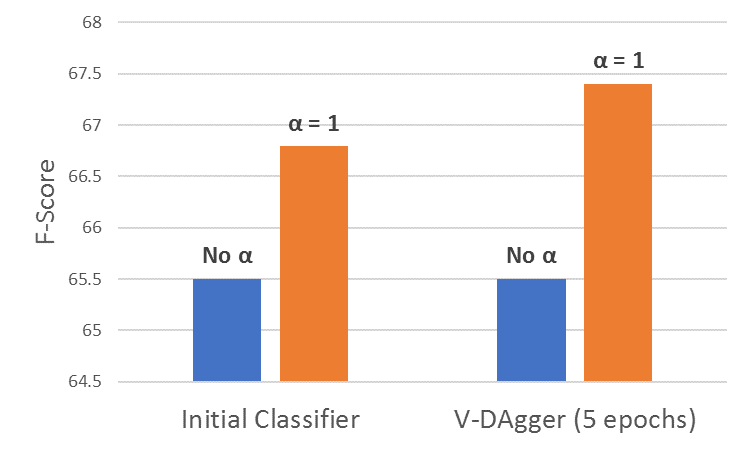
$a$-bound

Introduced by Khardon and Wachman (2007).

Reduce training noise by ignoring noisy training instances.

During training, if the classifier makes > $a$ mistakes on a training instance:

• Exclude instance from future training iterations.
• Related to Coaching (He et al., 2012)

$\alpha$-bound results

[Goodman et al. 2016](http://aclweb.org/anthology/P16-1001)

Comparison between IL approaches

[Goodman et al. 2016](http://aclweb.org/anthology/P16-1001)

Comparison against state of the art

[Goodman et al. 2016](http://aclweb.org/anthology/P16-1001)